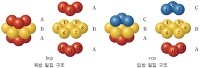
청과물 상인들은 경험을 통해서, 제한된 공간 내에 가장 많은 과일을 조밀하게 채우는 방법은 육방밀집쌓기-가운데의 과일을 중심으로 테두리에 6개, 아래와 위로 각각 3개씩의 과일을 배열하는 방법-를 이용하는 것임을 알고 있다. 그러나 수학자들은 다르다. 아무리 오랜 경험을 통해서 얻어진 사실이라고 해도 엄밀한 과정을 통해서 증명되기 전까지는 옳고 그름에 대한 판단을 유보한다. 수학자들의 이러한 태도를 가장 잘 보여 주는 사례가 ‘뉴턴과 그레고리의 논쟁’이다. 하나의 구(球)와 접할 수 있는 구의 최대의 수를 두고, 뉴턴은 12개만이 가능하다고 주장했고 그레고리는 13개까지도 가능하다고 주장했다. 육방밀집쌓기의 경우, 12개의 구가 가운데 구와 접하고 있을 뿐만 아니라 서로와도 모두 접하고 있기 때문에 추가..